Motivation
In computer graphics very often you want to know how big an object looks in screen, probably measured in pixels. Or at least you want to have an upper bound of the pixel coverage, because that allows you to perform intelligent Level of Detail (LOD) for that object. For example, if a character or a tree are not but a couple of pixels in screen, you probably want to render them with less detail (as in stochastic pruning of leaves for example).
One easy way to get an upper bound of the pixel coverage is to embed your object in a bounding box or sphere, the rasterize the sphere or box and count the amount of pixels. This requires complexity in your engine, and probably some delayed processing as the result of that rasterization won't be immedaitely ready. Modern hardware allows for conditional rendering, but still, the technique can only be applied in some cases. For example, it would be cool if a tessellation shader or a geometry shader would be able to tessellate or kill geometry (tree leaves) on the fly based on the pixel coverage of the object, just immediately.
Well, luckily for us there is a solution! The pixel coverage of a (bounding) sphere happens to have analytic expression can be solved with no more than one square root, it is very compact. I'm not sure why this is not used more often and is not more documented, because it is super helpful, or so I find it for my demos. This article is about this analytical and fast bounding sphere screen coverage calculation. Enjoy!

Exact pixel coverage computed analytically without rasterization/sampling
The maths
Without any loss of generality, we are going to work in camera space (origin is at the camera position, and the z axis points in the view direction). All the points x of a sphere or radius r centered at the position o is described by

and all the points in a ray going through our pinhole camera and passing by a point (x, y) in the view plane get described by
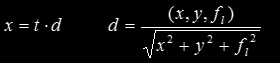
where fl is the focal length, and where we have already made sure that the ray is normalized such that |d|=1. A point in the view plane is covered by the projection of the sphere if the ray intersects with the sphere. This can be computed by substituting x for the ray in the equation of the sphere above, which results in the classic quadratic equation in t
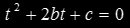
The quadratic has real solutions when the discriminant is positive,
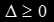 where
where 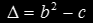 with
with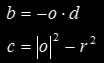
Expanding all the terms, the resulting inequality is
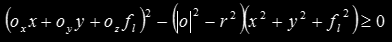
which can be rearranged by grouping the terms in x², y², xy, x, y and 1:
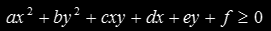

This is nothing but the implicit definition of an ellipse, since
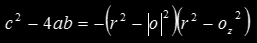
and this is a quantity always smaller than zero as long as the sphere doesn't contain the origin/camera, and as long the Z component of the sphere origin and eye point are separated by at least the sphere radius. So this inequality flags all the points in the plane (pixels in the screen if you want) that will get a projection (will get rasterized) by the sphere. Now we have to find a way to count those pixels!
Area counting
Luckily for us we can compute the area of ellipses easily if we know their geometric properties. Computing the center of the ellipse can be obtained in many ways, for example by making sure the derivatives of the implicit equal zero:

which gives
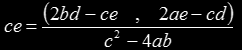
Once we replace the coefficients with the proper geometrical values, we get:
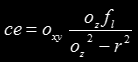
which is pretty compact. Once the center is obtained, one can translate the whole implicit function to the origin by a change of variable. Then, a rotation needs to be performed. The axis of the ellipse are going to be aligned to the (x,y) and (-y,x) directions respectively (or (d,e) and (-e,d) if you want. One can normalize these vectors by dividing by
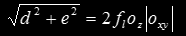
Once the rotation is performed, and once the axis of the ellipse align with the coordinate system, meaning the ellipse conforms to the standard form, one can proceed to compute the length of the axis and the area as usual. In the way there quite a few nice simplifications that happen, but I leave that as exercise to the reader ... (or look up the code in the Shadertoy link at the bottom of the article).
Implementation
The code is pretty small after all the simplifications:o-c:
float projectSphere( in vec4 sph, // sphere in world space
in mat4 cam, // camera matrix (world to camera)
in float fl ) // projection (focal length)
{
// transform to camera space
vec3 o = (cam*vec4(sph.xyz,1.0)).xyz;
float r2 = sph.w*sph.w;
float z2 = o.z*o.z;
float l2 = dot(o,o);
return -3.14159*fl*fl*r2*sqrt(abs((l2-r2)/(r2-z2)))/(r2-z2);
}
A realtime interactive implementation of the code above. Move the mouse or press "play". Click in the title to navgiate to the source code.