Intro
Here I will write some interesting facts about Value Noise (similar but not the same as Gradient Noise, of which Perlin Noise is one posible implementation). Yes, incredibly enough, you will find here some information that you cannot find anywhere else, not that much poeple speaks about the derivatives of the Value Noise, like how to calculate them analytically and what to do with them. So, why not to do it here? They are very useful after all. For example, I used them to create the landscape in the Elevated 4k demo. For Gradient Noise derivatives you can read this other article. So, let's see.
Noise derivatives are used to slightly modify the traditional fbm construction
in a very simple way. Note the much nicer variety obtained compared to a
regular fbm.
Analytical derivatives computation is much faster and more accurate than the
central differences method, and depending on the fractal sum function (ridged
noise, turbulence, etc), analytical normals can be computed for the complete
heightmap.
The image is rendered by directly raymarching the procedural function (no
normal maps, no materials), only diffuse lighting and fog are used.
in a very simple way. Note the much nicer variety obtained compared to a
regular fbm.
Analytical derivatives computation is much faster and more accurate than the
central differences method, and depending on the fractal sum function (ridged
noise, turbulence, etc), analytical normals can be computed for the complete
heightmap.
The image is rendered by directly raymarching the procedural function (no
normal maps, no materials), only diffuse lighting and fog are used.
The derivatives
Let's call our 3d Value Noise n(x,y,z). Everything it's the same for any amount of dimensions of course. We adopt the usual notation for derivatives
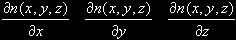 | or | 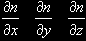 | in short. |
The (3d) noise function it's based on a (tri)linear interpolation of random values at some given latice points. Something like this:
n = lerp(w, lerp(v, lerp(u, a, b) ,lerp(u, c, d)),
lerp(v, lerp(u, e, f), lerp(u, g, h)));
where u(x), v(y), w(z) are normally a cubic or quintic polynomial of the form
u(x) = 3x2 - 2x3
or
u(x) = 6x5 - 15x4 + 10x3
Now, n(x,y,z) can be expanded as follows
n(u,v,w) = k0 + k1·u + k2·v + k3·w + k4·uv + k5·vw + k6·wu + k7·uvw
with
k0 = a
k1 = b - a
k2 = c - a
k3 = e - a
k4 = a - b - c + d
k5 = a - c - e + g
k6 = a - b - e + f
k7 = -a + b + c - d + e - f -g + h
The derivatives can now be computed easily, for example, for the x dimension:
∂n/∂x = (k1 + k4·v + k6·w + k7·vw)·u'(x)
with
u'(x) = 6·x·(1-x)
or
u'(x) = 30·x2(x2 - 2x + 1)
depending whether we chose the cubic or quintic u(x) function above.
Therefore it's very easy to make a function than returns the noise value and the three derivatives in one go, making it extremely cheap compared to the central difference method, that is 5 times slower.
// returns 3D value noise and its 3 derivatives
vec4 noised( in vec3 x )
{
vec3 p = floor(x);
vec3 w = fract(x);
vec3 u = w*w*w*(w*(w*6.0-15.0)+10.0);
vec3 du = 30.0*w*w*(w*(w-2.0)+1.0);
float a = myRandomMagic( p+vec3(0,0,0) );
float b = myRandomMagic( p+vec3(1,0,0) );
float c = myRandomMagic( p+vec3(0,1,0) );
float d = myRandomMagic( p+vec3(1,1,0) );
float e = myRandomMagic( p+vec3(0,0,1) );
float f = myRandomMagic( p+vec3(1,0,1) );
float g = myRandomMagic( p+vec3(0,1,1) );
float h = myRandomMagic( p+vec3(1,1,1) );
float k0 = a;
float k1 = b - a;
float k2 = c - a;
float k3 = e - a;
float k4 = a - b - c + d;
float k5 = a - c - e + g;
float k6 = a - b - e + f;
float k7 = - a + b + c - d + e - f - g + h;
return vec4( -1.0+2.0*(k0 + k1*u.x + k2*u.y + k3*u.z + k4*u.x*u.y + k5*u.y*u.z + k6*u.z*u.x + k7*u.x*u.y*u.z),
2.0* du * vec3( k1 + k4*u.y + k6*u.z + k7*u.y*u.z,
k2 + k5*u.z + k4*u.x + k7*u.z*u.x,
k3 + k6*u.x + k5*u.y + k7*u.x*u.y ) );
}
You can see an example of the code above here: https://www.shadertoy.com/view/XsXfRH
Fbm derivatives
The fBM (Fractional Brownian Motion) is normally implemented as a fractal sum of Value Noise functions.
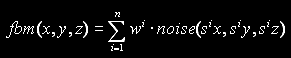
with w=1/2 and s=2, or something close, normally. When s=2 each iteration is called a "octave" - for the doubling of the frequency, like in music. The total derivative is in that case the weighted sum of the derivatives for each octave of course, as in regular derivative rules. If you implement a ridged Value Noise or other variations you can also easily drive the right way to combine the derivatives, unless you have a discontinuous shaping function like a fabsf().
// returns 3D fbm and its 3 derivatives
vec4 fbm( in vec3 x, int octaves )
{
float f = 1.98; // could be 2.0
float s = 0.49; // could be 0.5
float a = 0.0;
float b = 0.5;
vec3 d = vec3(0.0);
mat3 m = mat3(1.0,0.0,0.0,
0.0,1.0,0.0,
0.0,0.0,1.0);
for( int i=0; i < octaves; i++ )
{
vec4 n = noised(x);
a += b*n.x; // accumulate values
d += b*m*n.yzw; // accumulate derivatives
b *= s;
x = f*m3*x;
m = f*m3i*m;
}
return vec4( a, d );
}
Having derivatives available is useful for other purposes. For example, derivatives of noise allow to compute analytic normals without central differences. In the case of raymarching a terrain, this can be super useful if normals are needed at each raymarcing step (for example, to determine if trees grow or not at a given point based on slope). Similarly, when doing volumetric raymarching of clouds, having analytic normals (extracted form noise derivatives) without resporting to central differences can make the whole algorith up to 6x faster (depending how the central differences are inplemented).
This is a realtime raymarched landscape computed with analytical normals through value noise derivatives as explained in this article:

Source code: https://www.shadertoy.com/view/4ttSWf
This rock has surface normals computed analytically without central differences, by using the code above explained in this article:

Source code: https://www.shadertoy.com/view/XttSz2
Other uses
Another use of noise derivatives is to modify the fbm() construction to achieve different looks. For example, it is enough injecting the derivatives in the core of the fbm allows to simulate different erosion-like effects and creates some rich variety of shapes to the terrain, with flat areas as well as more rough areas (click to enlarge the images).
I rendered these images in 2008 with the code below. The image on the right uses the cubic version of u(x) while the one on the left uses the quintic. Note how the left image has some discontinuity artefacts, due to the non continuity of the second derivatives of u(x) and therefore of the fbm function.
const mat2 m = mat2(0.8,-0.6,0.6,0.8);
float terrain( in vec2 p )
{
float a = 0.0;
float b = 1.0;
vec2 d = vec2(0.0);
for( int i=0; i<15; i++ )
{
vec3 n=noised(p);
d +=n.yz;
a +=b*n.x/(1.0+dot(d,d));
b *=0.5;
p=m*p*2.0;
}
return a;
}
You can see the code live and in action in Shadertoy: https://www.shadertoy.com/view/MdX3Rr