Intro
Fog is very popular element in computer graphics, so popular that in fact we are always introduced to it early in textbooks or tutorials. However these textbooks, tutorials and even APIs only go as far as a simple distance based color blending, and stop there. Even advanced demos, interactive applications and games go no further that the simple color blending. Hopefully one can do much better and introduce some extra beauty and/or realism to the images with very little additional work on top of the basic idea.
Colored fog
Traditionally fog is introduced as being the visual element that gives distance cues in an image. And indeed the fog quickly helps us understand the distances and therefore scale of objects, and the world itself.

Without fog it's not easy to tell the scale of the terrain

With fog we immediately understand the size the terrain
vec3 applyFog( in vec3 col, // color of pixel
in float t ) // distance to point
{
float fogAmount = 1.0 - exp(-t*b);
vec3 fogColor = vec3(0.5,0.6,0.7);
return mix( col, fogColor, fogAmount );
}
vec3 applyFog( in vec3 col, // color of pixel
in float t, // distance to point
in vec3 rd, // camera to point
in vec3 lig ) // sun direction
{
float fogAmount = 1.0 - exp(-t*b);
float sunAmount = max( dot(rd, lig), 0.0 );
vec3 fogColor = mix( vec3(0.5,0.6,0.7), // blue
vec3(1.0,0.9,0.7), // yellow
pow(sunAmount,8.0) );
return mix( col, fogColor, fogAmount );
}
The effect can be done much more sophisticated. For example the exponent of the dot product between the sun and view vectors (which of course controls the influence of the directional color gradient) can be varyied with distance too. With the right settings one can fake glowing/blooming and other light scattering effects without actually doing any multipass or render to texture but a simple change to the fog equation. Color can change with altitude too, or any other parameters you might think of.

Regular monocrhome fog

Colored fog based on sun direction
Another variation of the technique that we can develop starts by first splitting the usual mix() command in its two parts, ie, replace
finalColor = mix( pixelColor, fogColor, 1.0-exp(-distance*b) );
with
finalColor = pixelColor*exp(-distance*b) + fogColor*(1.0-exp(-distance*b));
Then, according to classic CG atmospheric scattering papers, the first term could be interpreted as the absortion of light due to scattering or "extinction", and the second term can be interpreted as the "inscattering". We note that this way of expressing fog is more powerfull, because now we can choose independent fallof parameters b for the extinction and inscattering. Furthermore, we can have not one or two, but up to six different coefficients - three for the rgb channels of the extintion color and three for the rgb colored version of the inscattering.
vec3 extColor = vec3( exp(-distance*be.x), exp(-distance*be.y) exp(-distance*be.z) );
vec3 insColor = vec3( exp(-distance*bi.x), exp(-distance*bi.y) exp(-distance*bi.z) );
finalColor = pixelColor*(1.0-extColor) + fogColor*insColor;
This way of doing fog, combined with the sun direction coloring and other tricks can give you a very powerfull and simple fog system, yet very compact and fast. It's also quite intuitive, and you don't have to deal with tons of physics, maths and magic constants for Mie and Rayleight spectral constants and stuff. Simple and controlable is the win.
Non constant density
The original and simple fog formula has two parameters: the color and the density (which I called b in the shader code above). Same way we modified it to have non constant color, we can also modify it so it doesn't have constant density. I'm gonna follow Crytek's trick in this one, but you can play and get some cool results with your own formulas too, although the derivation in that case might be a bit more complex.
Real atmosphere is less dense in the height athmosphere than at the sea level. We can model that density variation with an exponential. The good thing of the exponential function is that the solution to the formulas is analytical. Let's see. We start with this exponential density function, which depends on the height y of our point:
d(y) = a⋅e-b⋅y
The parameter b controls, of course, the fallof of this density. Now, as our ray traverses the atmosphere from the camera to the point, it will be accumulating opacity as it traverses the athmosphere. The amount of fog it gathers in each of these infinite amount of infinitelly little steps is driven by the fog density (that we just defined) at those points. So we have to add them all together. But of course, adding an infinte amount of ridiculosuly small things is called "integral" in maths. So, given our ray
r(t) = oy + t⋅ky
we have that the total amount of fog is

where T is the distance from the camera to the point. This integral can be solved analytically, giving
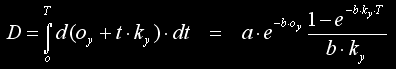
so that our non-constant-density-fog shader is
which means that by adding no more than one division to the original formula we can get some cool height based fog (note that the rest of the formula is constant for a given frame).
we have that the total amount of fog is

where T is the distance from the camera to the point. This integral can be solved analytically, giving
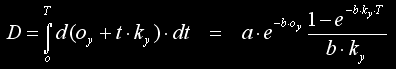
so that our non-constant-density-fog shader is
vec3 applyFog( in vec3 col, // color of pixel
in float t, // distnace to point
in vec3 ro, // camera position
in vec3 rd ) // camera to point vector
{
float fogAmount = (a/b) * exp(-ro.y*b) * (1.0-exp(-t*rd.y*b))/rd.y;
vec3 fogColor = vec3(0.5,0.6,0.7);
return mix( col, fogColor, fogAmount );
}
which means that by adding no more than one division to the original formula we can get some cool height based fog (note that the rest of the formula is constant for a given frame).

The integral of the fog density function d(y) over the ray gives the final amount of fog

Note low altitude parts get extra fog

Without height based fog
Again, there are many variations that one can add to this constanst-vertical-exponential-fallof-density-function shader.

A raymarched terrain with non constant fog density