Often, ellipses are usually not much more difficult than disks/circles, and one can compute lots of their properties analytically and easily, like their bounding boxes and intersections. However, some properties turn out to be a bit more complicated to compute than one would expect. One such property is the distance from a point to an ellipse, in 2D!
So, for a given point in the plane p={x,y} and a parametric ellipse q centered in the origin with radii a and b in the x and y axes, q(ω) = { a⋅cos ω, b⋅sin ω }, the square of the distance from p to the ellipse is
s2(ω) = |q(ω)-p|2
which expands to
s2(ω) = |q(ω)-p|2 = |q(ω)|2 - 2<q(ω),p> + |p|2 = a2⋅cos2ω + b2⋅sin2ω + x2 + y2 - 2(a⋅x⋅cos ω - b⋅y⋅sin ω)
The closest point will be for an ω such that
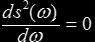
which expands to
(b2-a2)⋅sin ω⋅cos ω + ax⋅sin ω - by⋅cos ω = 0
This calls for the change of variable λ=cos(ω), so that
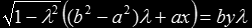
which expands into a quartic equation with the following coefficients:

or by dividing the equation by the leading coefficient k4 (the only condition to be able to do so is that the ellipse is not, in fact, a circle), and by then renaming ,
,
k4 = 1
k3 = 2m
k2 = m2 + n2 - 1
k1 = -2m
k0 = -m2
From this point on we proceed to resolve the quartic equation analytically with the standard method. Due to some of the symmetries in the coefficients, we get some pretty nice simplifications though. For example, the resolvent cubic equation loses its linear term and then depresses to
p3 - 3Qp + 2R = 0
with
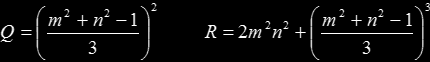
Due to all the symmetries mentioned, and the fact that we know we are looking only for real roots (possibly only one, if we are measuring the distance from a point outside the ellipse), the code gets quite compact. Also, we use the symmetry of the geometrical problem and we force our point to be on the first quadrant of the coordinate system (x>0 and y>0).
An interactive version (click and move the mouse over the ellipse to deform it) and reference code (click in the title of the viewport) can be found here:
Unfortunately, the analytical method is both expensive and not very stable, in that the root finder is difficult to keep under control when the ellipse is close to a circle or when it is very eccentric. As a result the distance computation returns wrong values sometimes.
An alternative is to consider a numeric solver. So, let's start computing the closes point to p on the ellipse, q. We know that the vector p-q will have to be perpendicular to the tangent of the ellipse at q. So, if we parametrize the ellipse again as q(ω) = { a⋅cos ω, b⋅sin ω }, then
<p-q(ω), q'(ω)> = 0
with q'(ω) being the tangent, which takes this form:
q'(ω) = { -a⋅sin ω, b⋅cos ω}
If we expand, we get the equation
f(ω) = -a⋅sin ω ⋅(x-a⋅cos ω) + b⋅cos ω ⋅(y-b⋅sin ω) = 0
which we are going to solve by using Newton-Raphson method, for which we need the derivative of the function above:
f'(ω) = -<p-u,v> - <v,v>
with
u = { a⋅cos ω, b⋅sin ω }
v = {-a⋅sin ω, b⋅cos ω }
So our iterative process will be
ωn+1 = ωn + <p-u,v> / (<p-u,u> + <v,v>)
The most difficult part is ensuring that the initial value of ω, ω0 makes the sequence converge to the desired root. An reasonable value for ω0 can be computed by stretching the space so the ellipse becomes a circle, computing the closest point from the stretched p to the circle, and then undoing the stretch:
ω0 = atan(a⋅y / b⋅x)
Because we are going to work only with the first quadrant of the plane (since the ellipse is symmetric anyways), this will be fine. In fact, the sequence will converge for all points in the exterior of the ellipse. Unfortunately, some point in the interior will not converge, and a different initial ω0 is required for them. In my implementation, I decided to select all the point below the line passing through the discontinuity of the gradient with slope (a,b), and make them start at ω0 = 0.
The code below implements this method to compute the distance to an ellipse (which you can also find here: https://www.shadertoy.com/view/4lsXDN:
The code above uses 5 iterations, which produces acceptable results. For some extremely eccentric ellipses the number of iterations might need to be increased. Assuming GPUs compute sin and cos of the same angle in a single instruction, and that this instruction is very fast (which it is), then the code above is not that bad compared to the analytic solver. But it is much more robust.
A variation of the above that doesn't use trigonometric functions and uses rotations instead (which is another way to think of the same concept), is the following code (which you can also find here: https://www.shadertoy.com/view/tttfzr:
This is the interactive version of the trigonometric solver aboce (click and move the mouse on the ellipse to deform the ellipse):
Method 1 - analytical (quartic equation)
So, for a given point in the plane p={x,y} and a parametric ellipse q centered in the origin with radii a and b in the x and y axes, q(ω) = { a⋅cos ω, b⋅sin ω }, the square of the distance from p to the ellipse is
s2(ω) = |q(ω)-p|2
which expands to
s2(ω) = |q(ω)-p|2 = |q(ω)|2 - 2<q(ω),p> + |p|2 = a2⋅cos2ω + b2⋅sin2ω + x2 + y2 - 2(a⋅x⋅cos ω - b⋅y⋅sin ω)
The closest point will be for an ω such that
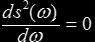
which expands to
(b2-a2)⋅sin ω⋅cos ω + ax⋅sin ω - by⋅cos ω = 0
This calls for the change of variable λ=cos(ω), so that
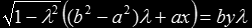
which expands into a quartic equation with the following coefficients:

or by dividing the equation by the leading coefficient k4 (the only condition to be able to do so is that the ellipse is not, in fact, a circle), and by then renaming
 ,
,k4 = 1
k3 = 2m
k2 = m2 + n2 - 1
k1 = -2m
k0 = -m2
From this point on we proceed to resolve the quartic equation analytically with the standard method. Due to some of the symmetries in the coefficients, we get some pretty nice simplifications though. For example, the resolvent cubic equation loses its linear term and then depresses to
p3 - 3Qp + 2R = 0
with
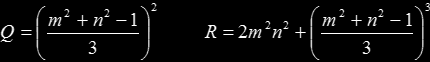
Due to all the symmetries mentioned, and the fact that we know we are looking only for real roots (possibly only one, if we are measuring the distance from a point outside the ellipse), the code gets quite compact. Also, we use the symmetry of the geometrical problem and we force our point to be on the first quadrant of the coordinate system (x>0 and y>0).
float sdEllipse( in vec2 p, in vec2 ab )
{
vec2 p = abs( p ); if( p.x>p.y ){ p=p.yx; ab=ab.yx; }
float l = ab.y*ab.y - ab.x*ab.x;
float m = ab.x*p.x/l; float m2 = m*m;
float n = ab.y*p.y/l; float n2 = n*n;
float c = (m2 + n2 - 1.0)/3.0; float c3 = c*c*c;
float q = c3 + m2*n2*2.0;
float d = c3 + m2*n2;
float g = m + m*n2;
float co;
if( d<0.0 )
{
float p = acos(q/c3)/3.0;
float s = cos(p);
float t = sin(p)*sqrt(3.0);
float rx = sqrt( -c*(s + t + 2.0) + m2 );
float ry = sqrt( -c*(s - t + 2.0) + m2 );
co = ( ry + sign(l)*rx + abs(g)/(rx*ry) - m)/2.0;
}
else
{
float h = 2.0*m*n*sqrt( d );
float s = sign(q+h)*pow( abs(q+h), 1.0/3.0 );
float u = sign(q-h)*pow( abs(q-h), 1.0/3.0 );
float rx = -s - u - c*4.0 + 2.0*m2;
float ry = (s - u)*sqrt(3.0);
float rm = sqrt( rx*rx + ry*ry );
float p = ry/sqrt(rm-rx);
co = (p + 2.0*g/rm - m)/2.0;
}
float si = sqrt( 1.0 - co*co );
vec2 q = vec2( ab.x*co, ab.y*si );
return length(q-p) * sign(p.y-q.y);
}
An interactive version (click and move the mouse over the ellipse to deform it) and reference code (click in the title of the viewport) can be found here:
Method 2 - Newton iterations
Unfortunately, the analytical method is both expensive and not very stable, in that the root finder is difficult to keep under control when the ellipse is close to a circle or when it is very eccentric. As a result the distance computation returns wrong values sometimes.
An alternative is to consider a numeric solver. So, let's start computing the closes point to p on the ellipse, q. We know that the vector p-q will have to be perpendicular to the tangent of the ellipse at q. So, if we parametrize the ellipse again as q(ω) = { a⋅cos ω, b⋅sin ω }, then
<p-q(ω), q'(ω)> = 0
with q'(ω) being the tangent, which takes this form:
q'(ω) = { -a⋅sin ω, b⋅cos ω}
If we expand, we get the equation
f(ω) = -a⋅sin ω ⋅(x-a⋅cos ω) + b⋅cos ω ⋅(y-b⋅sin ω) = 0
which we are going to solve by using Newton-Raphson method, for which we need the derivative of the function above:
f'(ω) = -<p-u,v> - <v,v>
with
u = { a⋅cos ω, b⋅sin ω }
v = {-a⋅sin ω, b⋅cos ω }
So our iterative process will be
ωn+1 = ωn + <p-u,v> / (<p-u,u> + <v,v>)
The most difficult part is ensuring that the initial value of ω, ω0 makes the sequence converge to the desired root. An reasonable value for ω0 can be computed by stretching the space so the ellipse becomes a circle, computing the closest point from the stretched p to the circle, and then undoing the stretch:
ω0 = atan(a⋅y / b⋅x)
Because we are going to work only with the first quadrant of the plane (since the ellipse is symmetric anyways), this will be fine. In fact, the sequence will converge for all points in the exterior of the ellipse. Unfortunately, some point in the interior will not converge, and a different initial ω0 is required for them. In my implementation, I decided to select all the point below the line passing through the discontinuity of the gradient with slope (a,b), and make them start at ω0 = 0.
The code below implements this method to compute the distance to an ellipse (which you can also find here: https://www.shadertoy.com/view/4lsXDN:
float sdEllipse( in vec2 p, in vec2 ab )
{
// symmetry
p = abs( p );
// determine in/out and initial omega value
bool s = dot(p/ab,p/ab)>1.0;
float w = s ? atan(p.y*ab.x, p.x*ab.y) :
((ab.x*(p.x-ab.x)<ab.y*(p.y-ab.y))? 1.5707963 : 0.0);
// find root with Newton solver
for( int i=0; i<5; i++ )
{
vec2 cs = vec2(cos(w),sin(w));
vec2 u = ab*vec2( cs.x,cs.y);
vec2 v = ab*vec2(-cs.y,cs.x);
w = w + dot(p-u,v)/(dot(p-u,u)+dot(v,v));
}
// compute final point and distance
return length(p-ab*vec2(cos(w),sin(w))) * (s?1.0:-1.0);
}
The code above uses 5 iterations, which produces acceptable results. For some extremely eccentric ellipses the number of iterations might need to be increased. Assuming GPUs compute sin and cos of the same angle in a single instruction, and that this instruction is very fast (which it is), then the code above is not that bad compared to the analytic solver. But it is much more robust.
A variation of the above that doesn't use trigonometric functions and uses rotations instead (which is another way to think of the same concept), is the following code (which you can also find here: https://www.shadertoy.com/view/tttfzr:
float sdEllipse( vec2 p, vec2 ab )
{
// symmetry
p = abs( p );
// initial value
vec2 q = ab*(p-ab);
vec2 cs = normalize( (q.x<q.y) ? vec2(0.01,1) : vec2(1,0.01) );
// find root with Newton solver
for( int i=0; i<5; i++ )
{
vec2 u = ab*vec2( cs.x,cs.y);
vec2 v = ab*vec2(-cs.y,cs.x);
float a = dot(p-u,v);
float c = dot(p-u,u) + dot(v,v);
float b = sqrt(c*c-a*a);
cs = vec2( cs.x*b-cs.y*a, cs.y*b+cs.x*a )/c;
}
// compute final point and distance
float d = length(p-ab*cs);
// return signed distance
return (dot(p/ab,p/ab)>1.0) ? d : -d;
}
This is the interactive version of the trigonometric solver aboce (click and move the mouse on the ellipse to deform the ellipse):