Computing the distance to a Julia set (or Mandelbrot set) of a polynomial is very useful, both for 2D and 3D (4D) fractal rendering algorithms. In 2D (complex domain), computing the distance enables the rasterization of the fractal without aliasing, because filtering is possible in cases where the area of the filled Julia set of Mandelbrot is too thin to be captured by point sampling inside the pixel, which happens most of the time. Having a distance also helps in 3D, where raymarching of SDFs can be used to efficiently rendering 3D Julia sets.

The Mandelbrot set rendered with the distance formula.

The Boettcher map φc(zo) applied to a grid pattern

The Hubbard-Douady potential Gc(zo)

The approximated SDF, dc(zo)

Approximated SDF for the Julia set of a degree 4 rational

A close up to a f(z)=z2+c Julia set.

A close up to a f(z)=z2+c Julia set.
This is a zoom animation I created in 2002 using this distance technique, which I leave here for my own historical reference:
As I mentioned, utilizing G(zo) and forcing it into getting closer to an euclidean distance through its linearized Taylor expansion
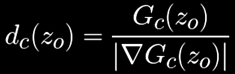
to get
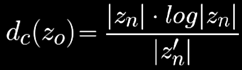
is just an approximation. In practice it's good enough for most applications, but that doesn't mean we shouldn't strive to do better, if a better way exists. In fact, mathematicians have come up with a better approximation (I removed all the subindices to make it easier to read):
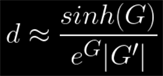
First, the formula above is usually given with a 1/2 factor in it and as a lower bound. For distance measurement purposes I have remove the 1/2 factor so it matches better with actual measurements.
Second, we can see right away that when close to the boundary of the fractal set G tends to zero, so the two formulas are in agreement there. Hopefully the formula derived by mathematicians is a better approximation to the true distance, when we move a bit away from the set. Well, let's see if that's true.
One way to check that would be to compute the real distance to a julia set through pixel scanning. While totally uncomplicated, there's an even nice way to do some tests.
While the Julia set of f(z)=z2+c is generally a fractal, the special cases c=0 and c=-2 are special indeed. So, for c=0 we get f(z)=z2 and the Julia set must the be boundary of the unit disk, since anything bigger than 1 (in length) will start growing uncontrollably and diverge to infinity, while anything smaller will converge rapidly to the fixed point 0. So in this case the Julia set of f(z) is not a fractal, but a circle. And computing the distance to a circle is pretty easy.
Similarly, although maybe less obviously, the case c=-2 is also not a fractal but a horizontal line segment of length 4 centered at the origin (repelling fixed points are -1 and 2, if you are interested). And we also know how to compute euclidean distances to line segments.
So let's go ahead and compare the distance approximations to the ground truth. In the bottom half of the image and on the top left and top right corners is the ground truth, the distance to the unit disk. At the top center left in desaturated yellow is the traditional approximated SDF (I'll call it SDF from now on even though it's not signed and cannot measure distances inside the set). On the top center right in saturated yellow is the better approximation.

Indeed, the traditional SDF works fine close to the circle but then quickly gets off track. On the other hand, the new SDF seems to behave really well, maybe even perfectly! That's great. Let's now compare the line segment Julia set for f(z)=z2-c

Unlike the previous one, this picture is disappointing. Both SDF approximations seem to deviate a lot from the ground truth, but the traditional one seems to stay closer to the real true distance for a little bit longer. So you might think that you could maybe pick one or the other depending on the particular Julia set you are rendering? So let's look a bit closer to their implementations.
In terms of computations there's not much of a difference, since the most expensive part of the overall distance computation is in the iterations of znthemselves, not so much in the final exponentials and logarithms in the expressions. Still, the better approximation can also be optimized using the properties of the logarithms like the third version here:
After optimizing the new approximation not only it gets cheaper, but also resembles a lot more then traditional one - the log has now been replaced with another expression that behaves similarly, but differently. But, besides this anecdotal fact, there's a very important thing to mention: the new approximation suffers a lot from precision issues. As n gets big (the number of iterations) k gets small, and that needs to be put together with lz2 which is big, resulting in an SDF of pretty bad quality, especially near the set where n is big and G is small, which is precisely where we need more precision (pun intended) for our renderer. I tried computing G indirectly through the sum of logarithms which you can find in some of the specialized literature, but that also didn't help, so overall it seems the traditional SDF which is also easier to derive is a better choice in most cases.
If you are going to use this SDF for raymarching, there's a small catch. As I quickly mentioned, mathematicians calculated that the SDF above is an approximation but might sometimes be slightly bigger than the actual distance, and that half of that approximation guarantees to be an upper bound for it. So, for raymarching purposes we'll use the formula above multiplied by 1/2.
It's also worth mentioning that the SDF above works for quaternions as well (4D), but that when rendering in 3D we usually just take one planar cut of it. In that case, the distance computed in quaternion space (4D) through the SDF above might be smaller than the actual distance the ray could travel in 3D. This is natural and happens with the projection of any shape from a higher dimensional space to a small one, which is obvious if you think of concave shapes.
There's a follow up article to this one dedicated to 4D Julia sets as well, and that having an SDF to the surface of the set naturally is what you need for raymarching them. Even though I won't expand on that in here and you should definitely go check those articles I just linked to, here goes an image of a pretty Julia set, cut in half, rendered with the traditional SDF derived in this article in Part 1:

A 3D (quaternion) Julia set rendered with the traditional distance formula

The Mandelbrot set rendered with the distance formula.
Part 1 - My basic approach
Without going into details in this article, here goes an intuitive and non-rigorous explanation of how we compute the distance to a Julia set. I'll compare this technique to a more mathematically correct one at the end of the article. But for now, given a polynomial map of degree p
zn+1 = znp + c
(where p=2 for the traditional Julia and Mandelbrot sets) we compute its Boettcher map as

This is an "uniformizating" deformation of the C plane. You can think of this map as follows: when far from the set, the znp term in f(z) = znp + c dominates over c. So, far away from c, zn+1 ≈ znp, and near infinity we can almost say that zn = zpn. Iterating all the way backwards (undoing all the iterations) as if c has never existed and the Julia set had been the unit circle all along can be done by computing znp-n.
So our Boettcher map deforms the plane in a way such that all the exterior of the Julia maps to the exterior of a unit disk (which is the Julia set for c=0). And it tends to the identity map

the further we move away from the set. Visually, it's a smooth deformation, like a blanket that attaches to the boundary of the set. You can find source code to compute it here: https://www.shadertoy.com/view/MdX3zN.
This map takes this form for any polynomial with any number of terms actually, not just monic ones, since the term zp always dominates near infinity.
zn+1 = znp + c
(where p=2 for the traditional Julia and Mandelbrot sets) we compute its Boettcher map as

This is an "uniformizating" deformation of the C plane. You can think of this map as follows: when far from the set, the znp term in f(z) = znp + c dominates over c. So, far away from c, zn+1 ≈ znp, and near infinity we can almost say that zn = zpn. Iterating all the way backwards (undoing all the iterations) as if c has never existed and the Julia set had been the unit circle all along can be done by computing znp-n.
So our Boettcher map deforms the plane in a way such that all the exterior of the Julia maps to the exterior of a unit disk (which is the Julia set for c=0). And it tends to the identity map

the further we move away from the set. Visually, it's a smooth deformation, like a blanket that attaches to the boundary of the set. You can find source code to compute it here: https://www.shadertoy.com/view/MdX3zN.
This map takes this form for any polynomial with any number of terms actually, not just monic ones, since the term zp always dominates near infinity.

The Boettcher map φc(zo) applied to a grid pattern
The Hubbard-Douady potential is the logarithm of the modulo of the Boettcher map, and can be seen as similar to the electric potential of a cylindrical charge (usually for a Julia set that is the unit circle, now for any Julia set of any shape thanks to the uniformizing Boettcher map):
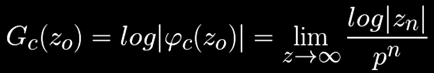
This is a smooth function, evaluates to zero inside the set (since zn won't diverge by definition but the denominator pn grows without bounds). It actually tends to zero as we get closer to the boundary of the set and grows approximately towards log|zo| as we move far away from the set (since the uniforming Boettcher map φ(c) tends to the identity):
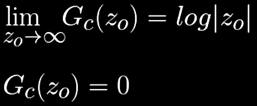
So, this function behaves a bit as a distance, in that it reaches zero exactly at the boundary of the Julia set, and increases the further we are from it. It is not a metric though, but we can try to fix it. For that, we can use the usual technique of dividing the function by the length of its gradient to approximate distances to the isosurfaces (it's like reversing a first order Taylor approximation really):
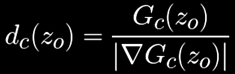
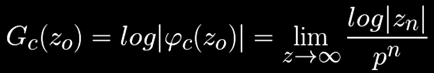
This is a smooth function, evaluates to zero inside the set (since zn won't diverge by definition but the denominator pn grows without bounds). It actually tends to zero as we get closer to the boundary of the set and grows approximately towards log|zo| as we move far away from the set (since the uniforming Boettcher map φ(c) tends to the identity):
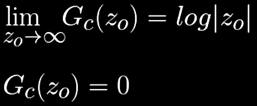
So, this function behaves a bit as a distance, in that it reaches zero exactly at the boundary of the Julia set, and increases the further we are from it. It is not a metric though, but we can try to fix it. For that, we can use the usual technique of dividing the function by the length of its gradient to approximate distances to the isosurfaces (it's like reversing a first order Taylor approximation really):
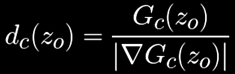

The Hubbard-Douady potential Gc(zo)
Computing the derivative of the logarithm, and canceling some terms, results in
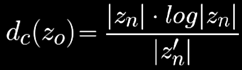
Basically this means than during our regular iteration loop we need to keep track of both zn as usual and of its derivative z'n. If we are rendering the generalized Mandelbrot set with
zn+1 = znp + c
then simple derivation rules give
z'n+1 = p⋅ znp-1⋅ z'n with z'0 = 1
and for a Mandelbrot set,
z'n+1 = p⋅ znp-1⋅ z'n + 1 with z'0 = 0
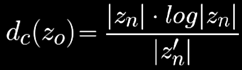
Basically this means than during our regular iteration loop we need to keep track of both zn as usual and of its derivative z'n. If we are rendering the generalized Mandelbrot set with
zn+1 = znp + c
then simple derivation rules give
z'n+1 = p⋅ znp-1⋅ z'n with z'0 = 1
and for a Mandelbrot set,
z'n+1 = p⋅ znp-1⋅ z'n + 1 with z'0 = 0

The approximated SDF, dc(zo)
As said, this work for any rational Mandelbrot or Julia set. The image to the right was computed with this algorithm for the Julia set of f(z) = (z-(1+i)/10)⋅(z-i)⋅(z-1)4 / ((z+1)⋅(z-(1+i)) + c, which is a rational function of degree 4. You can find the source code and realtime online demo for that image here: https://www.shadertoy.com/view/4dXGDX.
So for a traditional Julia set we'd compute the distance as follows:
So for a traditional Julia set we'd compute the distance as follows:
float calcDistance( complex z0, complex c )
{
complex z = zo;
complex dz = complex( 1.0, 0.0 );
float m2;
for( int i=0; i<1024; i++ )
{
dz = 2.0*z*dz;
z = z*z + c;
m2 = modulo_squared(z);
if( m2 > 1e20 ) break;
}
return sqrt( m2/modulo_squared(dz) )*0.5*log(m2);
}

Approximated SDF for the Julia set of a degree 4 rational
You can find this source code in action in this realtime shader: https://www.shadertoy.com/view/Mss3R8.
Now, note three things: one, we are using complex multiplications for z and dz, of course. Two, we changed the traditional bailout threshold (2 for a quadratic Julia set) to 1e10, since for our definition of G we need |z| to be big. Three, not only we avoided the square root inside the loop, but also saved one more in the computation of d through the properties of the logarithm.
Now, the following is a neat optimization that only applies to Julia sets and that I apply often: since all we need in our distance computation is the length of |z'n|, we don't need to track the whole complex or quaternion number z'. Instead we can just track its length right from the beginning. We can even only track the square of the length and avoid square roots as well. So, for a traditional z2+c Julia set:
|z'n+1|2 = 4|zn|2⋅|z'n|2
|z'0| = 1
which would translate into:
You can see this optimization in action in this realtime shader with source code, which was used to compute the images to the right: https://www.shadertoy.com/view/Mss3R8. The equivalent realtime animation and code for the Mandelbrot can be found here: https://www.shadertoy.com/view/lsX3W4
Now, note three things: one, we are using complex multiplications for z and dz, of course. Two, we changed the traditional bailout threshold (2 for a quadratic Julia set) to 1e10, since for our definition of G we need |z| to be big. Three, not only we avoided the square root inside the loop, but also saved one more in the computation of d through the properties of the logarithm.
Now, the following is a neat optimization that only applies to Julia sets and that I apply often: since all we need in our distance computation is the length of |z'n|, we don't need to track the whole complex or quaternion number z'. Instead we can just track its length right from the beginning. We can even only track the square of the length and avoid square roots as well. So, for a traditional z2+c Julia set:
|z'n+1|2 = 4|zn|2⋅|z'n|2
|z'0| = 1
which would translate into:
float calcDistance( complex z0, complex c )
{
complex z = zo;
float d2 = 1.0;
float m2;
for( int i=0; i<1024; i++ )
{
d2 *= 4.0*m2;
z = z*z + c;
m2 = modulo_squared(z);
if( m2 > 1e20 ) break;
}
return sqrt(m2/d2)*0.5*log(m2);
}
You can see this optimization in action in this realtime shader with source code, which was used to compute the images to the right: https://www.shadertoy.com/view/Mss3R8. The equivalent realtime animation and code for the Mandelbrot can be found here: https://www.shadertoy.com/view/lsX3W4

A close up to a f(z)=z2+c Julia set.

A close up to a f(z)=z2+c Julia set.
This is a zoom animation I created in 2002 using this distance technique, which I leave here for my own historical reference:
Part 2 - Comparison to the mathematical state of the art
As I mentioned, utilizing G(zo) and forcing it into getting closer to an euclidean distance through its linearized Taylor expansion
to get
is just an approximation. In practice it's good enough for most applications, but that doesn't mean we shouldn't strive to do better, if a better way exists. In fact, mathematicians have come up with a better approximation (I removed all the subindices to make it easier to read):
First, the formula above is usually given with a 1/2 factor in it and as a lower bound. For distance measurement purposes I have remove the 1/2 factor so it matches better with actual measurements.
Second, we can see right away that when close to the boundary of the fractal set G tends to zero, so the two formulas are in agreement there. Hopefully the formula derived by mathematicians is a better approximation to the true distance, when we move a bit away from the set. Well, let's see if that's true.
One way to check that would be to compute the real distance to a julia set through pixel scanning. While totally uncomplicated, there's an even nice way to do some tests.
While the Julia set of f(z)=z2+c is generally a fractal, the special cases c=0 and c=-2 are special indeed. So, for c=0 we get f(z)=z2 and the Julia set must the be boundary of the unit disk, since anything bigger than 1 (in length) will start growing uncontrollably and diverge to infinity, while anything smaller will converge rapidly to the fixed point 0. So in this case the Julia set of f(z) is not a fractal, but a circle. And computing the distance to a circle is pretty easy.
Similarly, although maybe less obviously, the case c=-2 is also not a fractal but a horizontal line segment of length 4 centered at the origin (repelling fixed points are -1 and 2, if you are interested). And we also know how to compute euclidean distances to line segments.
So let's go ahead and compare the distance approximations to the ground truth. In the bottom half of the image and on the top left and top right corners is the ground truth, the distance to the unit disk. At the top center left in desaturated yellow is the traditional approximated SDF (I'll call it SDF from now on even though it's not signed and cannot measure distances inside the set). On the top center right in saturated yellow is the better approximation.

Indeed, the traditional SDF works fine close to the circle but then quickly gets off track. On the other hand, the new SDF seems to behave really well, maybe even perfectly! That's great. Let's now compare the line segment Julia set for f(z)=z2-c

Unlike the previous one, this picture is disappointing. Both SDF approximations seem to deviate a lot from the ground truth, but the traditional one seems to stay closer to the real true distance for a little bit longer. So you might think that you could maybe pick one or the other depending on the particular Julia set you are rendering? So let's look a bit closer to their implementations.
In terms of computations there's not much of a difference, since the most expensive part of the overall distance computation is in the iterations of znthemselves, not so much in the final exponentials and logarithms in the expressions. Still, the better approximation can also be optimized using the properties of the logarithms like the third version here:
// traditional version
float d = 0.5*sqrt(lz2/ld2)*log(lz2);
// new approximation, direct
float k = exp2(-n);
float g = k*log(sqrt(lz2));
float ldg = k*sqrt(ld2/lz2);
d = sinh(g)/(ldg*exp(g));
// new approximation, optimized
float k = exp2(-n);
d = 0.5*sqrt(lz2/ld2)*(1.0-pow(lz2,-k))/k;
After optimizing the new approximation not only it gets cheaper, but also resembles a lot more then traditional one - the log has now been replaced with another expression that behaves similarly, but differently. But, besides this anecdotal fact, there's a very important thing to mention: the new approximation suffers a lot from precision issues. As n gets big (the number of iterations) k gets small, and that needs to be put together with lz2 which is big, resulting in an SDF of pretty bad quality, especially near the set where n is big and G is small, which is precisely where we need more precision (pun intended) for our renderer. I tried computing G indirectly through the sum of logarithms which you can find in some of the specialized literature, but that also didn't help, so overall it seems the traditional SDF which is also easier to derive is a better choice in most cases.
Part 3 - Final words
If you are going to use this SDF for raymarching, there's a small catch. As I quickly mentioned, mathematicians calculated that the SDF above is an approximation but might sometimes be slightly bigger than the actual distance, and that half of that approximation guarantees to be an upper bound for it. So, for raymarching purposes we'll use the formula above multiplied by 1/2.
It's also worth mentioning that the SDF above works for quaternions as well (4D), but that when rendering in 3D we usually just take one planar cut of it. In that case, the distance computed in quaternion space (4D) through the SDF above might be smaller than the actual distance the ray could travel in 3D. This is natural and happens with the projection of any shape from a higher dimensional space to a small one, which is obvious if you think of concave shapes.
There's a follow up article to this one dedicated to 4D Julia sets as well, and that having an SDF to the surface of the set naturally is what you need for raymarching them. Even though I won't expand on that in here and you should definitely go check those articles I just linked to, here goes an image of a pretty Julia set, cut in half, rendered with the traditional SDF derived in this article in Part 1:

A 3D (quaternion) Julia set rendered with the traditional distance formula