Intro
In the same way you can compute analytic occlusion for spheres, you can also compute it for boxes. Since the box is made of 6 quads, we need to determine which are the sides facing our shading point and compute their occlusion. Since the box is a convex object and non of the faces' projection overlap, we can calculate the occlusion contribution of each face individually and then simply sum them up all together.

Analytic occlusion for a box
The occlusion of a quad can be computer, just like for the sphere, as a double integral over the quad shape of the dot of the differential area element and the position vector, divided by the square length of the position vector and all modulated by the dot of the position and the normal at the shading point. The maths are involved and I failed to derive it in a few minutes, but some hints go here: [1] we can reduce the double integral over the surface to a line integral over the perimeter of the quad, using Green's Theorem. [2] since the perimeter is piece-wise linear, the line integral reduces to a sum over the four sides.
Each of of the four sides contributes proportionally to the length of the side projected to the unit hemisphere, which is the angle of the arc itslef, which you can compute as the acos of dot product of the vectors going to the two vertices of the edge. The cosine shading contribution comes from the angle between the normal of the triangle connecting the edge to the point under occlusion and the normal at the point.
The final expression can be found at the very bottom of page 41 of the Global Illumination Total Compendium:
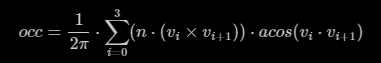
where the vertices are of course relative to the point under occlusion and must be normalized:
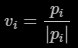
Code
For a box completely aboe the horizon of a point under shading, all we have to do is to evaluate the formula above per face. Of course, since we are integrating by edges, we can reuse much of the work across faces that share edges. So the above formula needs to be computed only 12 times, if the implementation is branchless. Then, based on which of the 6 faces of the box face the shading point we can add the contribution as needed:
float boxOcclusion( in vec3 pos, in vec3 nor, in vec3 box[8] )
{
// 8 points
vec3 v[0] = normalize( box[0] );
vec3 v[1] = normalize( box[1] );
vec3 v[2] = normalize( box[2] );
vec3 v[3] = normalize( box[3] );
vec3 v[4] = normalize( box[4] );
vec3 v[5] = normalize( box[5] );
vec3 v[6] = normalize( box[6] );
vec3 v[7] = normalize( box[7] );
// 12 edges
float k02 = dot( n, normalize( cross(v[2],v[0])) ) * acos( dot(v[0],v[2]) );
float k23 = dot( n, normalize( cross(v[3],v[2])) ) * acos( dot(v[2],v[3]) );
float k31 = dot( n, normalize( cross(v[1],v[3])) ) * acos( dot(v[3],v[1]) );
float k10 = dot( n, normalize( cross(v[0],v[1])) ) * acos( dot(v[1],v[0]) );
float k45 = dot( n, normalize( cross(v[5],v[4])) ) * acos( dot(v[4],v[5]) );
float k57 = dot( n, normalize( cross(v[7],v[5])) ) * acos( dot(v[5],v[7]) );
float k76 = dot( n, normalize( cross(v[6],v[7])) ) * acos( dot(v[7],v[6]) );
float k37 = dot( n, normalize( cross(v[7],v[3])) ) * acos( dot(v[3],v[7]) );
float k64 = dot( n, normalize( cross(v[4],v[6])) ) * acos( dot(v[6],v[4]) );
float k51 = dot( n, normalize( cross(v[1],v[5])) ) * acos( dot(v[5],v[1]) );
float k04 = dot( n, normalize( cross(v[4],v[0])) ) * acos( dot(v[0],v[4]) );
float k62 = dot( n, normalize( cross(v[2],v[6])) ) * acos( dot(v[6],v[2]) );
// 6 faces
float occ = 0.0;
occ += ( k02 + k23 + k31 + k10) * step( 0.0, v0.z );
occ += ( k45 + k57 + k76 + k64) * step( 0.0, -v4.z );
occ += ( k51 - k31 + k37 - k57) * step( 0.0, -v5.x );
occ += ( k04 - k64 + k62 - k02) * step( 0.0, v0.x );
occ += (-k76 - k37 - k23 - k62) * step( 0.0, -v6.y );
occ += (-k10 - k51 - k45 - k04) * step( 0.0, v0.y );
return occ / 6.283185;
}
There's a live example in Shadertoy of this code: https://www.shadertoy.com/view/4djXDy
With clipping
If you expect your box to be only partially visible then the strategy has to change a little bit, since you need to clip the faces (edges) of the box to the half plane defined by the normal and the point under the occlusion.

Analytic occlusion for a clipped box
The slow way to do this is to break up the box in 12 triangle and compute the occlusion for each one of them with clipping considerations. See here for an example: https://www.shadertoy.com/view/4sSXDV. A more smart alternative is to clip the 12 edges first and produce a new set of edges and faces, then perform the occlusion on them. In any case, this is an example of computing the analytic occlusion for a potentially clipped triangle:
float triOcclusionWithClipping( in vec3 pos, in vec3 nor, in vec3 v0, in vec3 v1, in vec3 v2, in vec4 plane )
{
if( dot( v0-pos, cross(v1-v0,v2-v0) ) < 0.0 ) return 0.0; // back facing
float s0 = dot( vec4(v0,1.0), plane );
float s1 = dot( vec4(v1,1.0), plane );
float s2 = dot( vec4(v2,1.0), plane );
float sn = sign(s0) + sign(s1) + sign(s2);
vec3 c0 = clip( v0, v1, plane );
vec3 c1 = clip( v1, v2, plane );
vec3 c2 = clip( v2, v0, plane );
// 3 (all) vertices above horizon
if( sn>2.0 )
{
return ftriOcclusion( pos, nor, v0, v1, v2 );
}
// 2 vertices above horizon
else if( sn>0.0 )
{
vec3 pa, pb, pc, pd;
if( s0<0.0 ) { pa = c0; pb = v1; pc = v2; pd = c2; }
else if( s1<0.0 ) { pa = c1; pb = v2; pc = v0; pd = c0; }
else/*if( s2<0.0 )*/{ pa = c2; pb = v0; pc = v1; pd = c1; }
return fquadOcclusion( pos, nor, pa, pb, pc, pd );
}
// 1 vertex above horizon
else if( sn>-2.0 )
{
vec3 pa, pb, pc;
if( s0>0.0 ) { pa = c2; pb = v0; pc = c0; }
else if( s1>0.0 ) { pa = c0; pb = v1; pc = c1; }
else/*if( s2>0.0 )*/ { pa = c1; pb = v2; pc = c2; }
return ftriOcclusion( pos, nor, pa, pb, pc );
}
// zero (no) vertices above horizon
return 0.0;
}
with the following functions being the fully-visible triangle and quad analytic occlusion functions
// fully visible front facing Triangle occlusion
float ftriOcclusion( in vec3 pos, in vec3 nor, in vec3 v0, in vec3 v1, in vec3 v2 )
{
vec3 a = normalize( v0 - pos );
vec3 b = normalize( v1 - pos );
vec3 c = normalize( v2 - pos );
return (dot( nor, normalize( cross(a,b)) ) * acos( dot(a,b) ) +
dot( nor, normalize( cross(b,c)) ) * acos( dot(b,c) ) +
dot( nor, normalize( cross(c,a)) ) * acos( dot(c,a) ) ) / 6.283185;
}
// fully visible front acing Quad occlusion
float fquadOcclusion( in vec3 pos, in vec3 nor, in vec3 v0, in vec3 v1, in vec3 v2, in vec3 v3 )
{
vec3 a = normalize( v0 - pos );
vec3 b = normalize( v1 - pos );
vec3 c = normalize( v2 - pos );
vec3 d = normalize( v3 - pos );
return (dot( nor, normalize( cross(a,b)) ) * acos( dot(a,b) ) +
dot( nor, normalize( cross(b,c)) ) * acos( dot(b,c) ) +
dot( nor, normalize( cross(c,d)) ) * acos( dot(c,d) ) +
dot( nor, normalize( cross(d,a)) ) * acos( dot(d,a) ) ) / 6.283185;
}
As usual with inverse trigonometrics, it wouldn't be a bad idea to do a clamp( x, -1.0, 1.0) on the argument of the acos() function before calling it.