Intro
Bezier curves are useful primitives for computer graphics. From hair to font types, they show up almost everywhere. Having their bounding box computed quickly is important for keeping them organized spatially for fast query or evaluation. While simple approximations to the bbox are trivial (such as computing the bounding box of their control points), in this article we deduce the exact bounding box analytically.
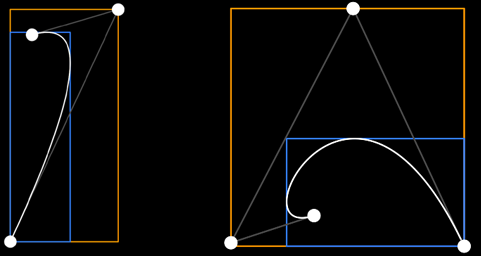
control points in yellow, and their exact bounding box in blue

Quadratic Bezier
We start with a quadratic Bezier segment passing through points p0 and p2 and tangent control point p1, defined by
p(t) = (1-t)2⋅p0 + 2⋅(1-t)⋅t⋅p1 + t2⋅p2
We know its bounding box is equal or smaller to the bounding box of the convex hull defined by its three control points p0, p1 and p2 - the whole curve must be contained within the convex hull of the control points, since the weights of each control point add up to exactly 1:
(1-t)2 + 2⋅(1-t)⋅t + t2 = 1
We note that if p1 happens to be inside the bounding box defined by p0 and p2, we are done because that's the bounding box of the whole Bezier segment. If p1 is outside of it, then the bounding box of the segment will be smaller than the bounding box of the three control points but bigger than the bounding box defined by p0 and p2. In order to find the exact extent of it, all we need to do is compute the maxima/minima of the segment's coordinates at some point along the curve, which we can do by computing the curve's derivative
p'(t) = t⋅(2p0 - 4p1 + 2p2) + 2⋅(p1-p0)
and equating it to 0, which results in
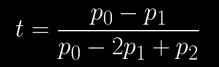
where the division here is expressing a component-wise division. Meaning, for a 2D bezier segment, we'll evaluate the above equation for the x and y components of p0, p1 and p2, resulting in two values for t, which when plugged back in the formula for the Bezier segment p(t) will give us our min/max bbox extent.
The code to perform the above could look like the following:
vec4 bboxBezier(in vec2 p0, in vec2 p1, in vec2 p2 )
{
vec2 mi = min(p0,p2);
vec2 ma = max(p0,p2);
if( p1.x<mi.x || p1.x>ma.x || p1.y<mi.y || p1.y>ma.y )
{
vec2 t = clamp((p0-p1)/(p0-2.0*p1+p2),0.0,1.0);
vec2 s = 1.0 - t;
vec2 q = s*s*p0 + 2.0*s*t*p1 + t*t*p2;
mi = min(mi,q);
ma = max(ma,q);
}
return vec4( mi, ma );
}
Needless to say that for a 3D quadratic Bezier segment the code is basically the same, but extending all data types to vec3 and the inner bounding box test to a 3D test.
This code is relatively fast, it contains a few multiplications and one division, and in most cases the savings in bounding space are pretty big. This is a reference implementation running in realtime: https://www.shadertoy.com/view/lsyfWc
Cubic Bezier
The process to compute the bounding box of a cubic Bezier segment is analogous. The derivative becomes a second degree polynomial, which of course has also an analytic solution involving one square root. So, lets see:
p(t) = (1-t)3⋅p0 + 3⋅(1-t)2⋅t⋅p1 + 3⋅(1-t)⋅t2⋅p2 + t3⋅p3
Again the base functions follow the binomial coefficients, and add up to 1. The derivative of the curve is actual a second degree bezier curve itself, with tangents as control points:
p'(t)/3 = (1-t)2⋅(p1-p0) + 2⋅(1-t)⋅t⋅(p2-p1) + t2⋅(p3-p2)
Note I divided the derivative by 3 to make it easier to recognize it as a second degree Bezier, since we don't care about constant factor anyways for our minima/maxima search. Speaking of what, equating the derivative with zero gives us a quadratic equation of the form
at2 + 2bt + c = 0
with of course
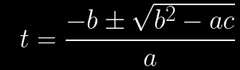
where
a = -1⋅p0 + 3⋅p1 - 3⋅p2 + 1⋅p3
b = 1⋅p0 - 2⋅p1 + 1⋅p2
c = -1⋅p0 + 1⋅p1
and the three coefficients are vectors really (for we are working in N dimensions, so the above quadratic are really N simultaneous quadratic equations to be solved). Also, these coefficients show yet again one more way the Bezier curves are related to Pascals's triangle. If we rewrite the above as a matrix multiplication it might be more obvious:

where k is a Nx2 matrix.
Now with all the quadratics in place, we are ready to solve the equation and compute our analytically perfect and tight bounding box (in this case, for a 2D curve)!
vec4 bboxBezier(in vec2 p0, in vec2 p1, in vec2 p2, in vec2 p3 )
{
vec2 mi = min(p0,p3);
vec2 ma = max(p0,p3);
vec2 c = -1.0*p0 + 1.0*p1;
vec2 b = 1.0*p0 - 2.0*p1 + 1.0*p2;
vec2 a = -1.0*p0 + 3.0*p1 - 3.0*p2 + 1.0*p3;
vec2 h = b*b - a*c;
if( h.x > 0.0 )
{
h.x = sqrt(h.x);
float t = (-b.x - h.x)/a.x;
if( t>0.0 && t<1.0 )
{
float s = 1.0-t;
float q = s*s*s*p0.x + 3.0*s*s*t*p1.x + 3.0*s*t*t*p2.x + t*t*t*p3.x;
mi.x = min(mi.x,q);
ma.x = max(ma.x,q);
}
t = (-b.x + h.x)/a.x;
if( t>0.0 && t<1.0 )
{
float s = 1.0-t;
float q = s*s*s*p0.x + 3.0*s*s*t*p1.x + 3.0*s*t*t*p2.x + t*t*t*p3.x;
mi.x = min(mi.x,q);
ma.x = max(ma.x,q);
}
}
if( h.y>0.0 )
{
h.y = sqrt(h.y);
float t = (-b.y - h.y)/a.y;
if( t>0.0 && t<1.0 )
{
float s = 1.0-t;
float q = s*s*s*p0.y + 3.0*s*s*t*p1.y + 3.0*s*t*t*p2.y + t*t*t*p3.y;
mi.y = min(mi.y,q);
ma.y = max(ma.y,q);
}
t = (-b.y + h.y)/a.y;
if( t>0.0 && t<1.0 )
{
float s = 1.0-t;
float q = s*s*s*p0.y + 3.0*s*s*t*p1.y + 3.0*s*t*t*p2.y + t*t*t*p3.y;
mi.y = min(mi.y,q);
ma.y = max(ma.y,q);
}
}
return vec4( mi, ma );
}
Or if a more compact (but more wasteful in most architectures) is your thing, then
vec4 bboxBezier(in vec2 p0, in vec2 p1, in vec2 p2, in vec2 p3 )
{
vec2 mi = min(p0,p3);
vec2 ma = max(p0,p3);
vec2 c = -1.0*p0 + 1.0*p1;
vec2 b = 1.0*p0 - 2.0*p1 + 1.0*p2;
vec2 a = -1.0*p0 + 3.0*p1 - 3.0*p2 + 1.0*p3;
vec2 h = b*b - a*c;
if( any(greaterThan(h,vec2(0.0))))
{
vec2 g = sqrt(abs(h));
vec2 t1 = clamp((-b - g)/a,0.0,1.0); vec2 s1 = 1.0-t1;
vec2 t2 = clamp((-b + g)/a,0.0,1.0); vec2 s2 = 1.0-t2;
vec2 q1 = s1*s1*s1*p0 + 3.0*s1*s1*t1*p1 + 3.0*s1*t1*t1*p2 + t1*t1*t1*p3;
vec2 q2 = s2*s2*s2*p0 + 3.0*s2*s2*t2*p1 + 3.0*s2*t2*t2*p2 + t2*t2*t2*p3;
if( h.x>0.0 )
{
mi.x = min(mi.x,min(q1.x,q2.x));
ma.x = max(ma.x,max(q1.x,q2.x));
}
if( h.y>0.0 )
{
mi.y = min(mi.y,min(q1.y,q2.y));
ma.y = max(ma.y,max(q1.y,q2.y));
}
}
return vec4( mi, ma );
}
Either way, you have a realtime running reference code here: https://www.shadertoy.com/view/XdVBWd
3D
Extending the above code to 3D is trivial, you just need to perform the same computations simply by replacing all vec2 variables by vec3 types, and then performing the min and max techs in x, y and z. Youcan find some reference code here: https://www.shadertoy.com/view/MdKBWt